La vie sexuelle des punaises
Rappel de l'énoncé
Les punaises sont des animaux ponctuels qui vivent dans le plan. Il y a des punaises mâles et des punaises femelles. Un accouplement entre un mâle situé en un point $M$ et une femelle située en un point $F$ consiste simplement à tracer le segment $[FM]$, et cet accouplement ne peut avoir lieu que sous la condition d'intimité suivante : aucun segment tracé par un autre accouplement ne doit croiser le segment $[FM]$.
On donne une population de 5 millions de punaises femelles et 5 millions de punaises mâles, en «position générale» (jamais plus de 2 punaises sur une même droite). Prouver qu'il est possible de réaliser 5 millions d'accouplements simultanément !
Solution
On considère toutes les façons possibles de relier 2 à 2 par un segment les 5 millions de punaises femelles aux 5 millions de punaises mâles (sans tenir compte de la condition d'intimité). Parmi toutes ces configurations, on considère celle (ou une de celles) qui réalise(nt) le minimum de la somme des longueurs des 5 millions de segments. Pour celle-ci, la condition d'intimité est réalisée. En effet, si deux segments $[MF]$ et $[M\prime F\prime]$ tracés dans cette configuration se rencontraient en un point $I$, on aurait
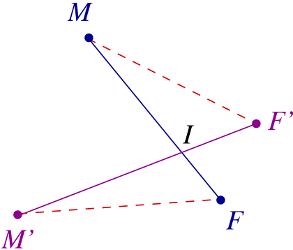$$ MF + M\prime F\prime = MI+IF + M\prime I+IF\prime $$
$$ = (MI+IF\prime ) + (M\prime I+IF) > MF\prime + M\prime F,$$
et donc on pourrait trouver une autre configuration avec une somme de longueurs strictement inférieure.
