How do random Fibonacci sequences grow?
Overview of the article
In this paper, we study two kinds of random Fibonacci sequences defined by F1 = F2 =1 , and, for n > 0 , Fn+1 = Fn +/- Fn-1 (linear case) or Fn+1 = | Fn +/- Fn-1 | (non-linear case) where each +/- sign is independent and either + with probability p or - with probability 1-p (0 < p ≤ 1 ).
We are mainly interested in the exponential growth (largest Lyapunov exponent) of these sequences. We show that these largest Lyapunov exponents can be computed as an integral with respect to some explicit probabity measure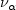 
defined inductively on Stern-Brocot intervals (see the figure below).
Linear case
For all 0 < p ≤ 1, with probability 1, n-1log |Fn| goes, as n goes to infinity, to
where
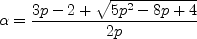
Non-linear case
For p ≤ 1/3, with probability 1, n-1log |Fn| goes to zero, as n goes to infinity.
For all p ≥ 1/3, with probability 1, n-1log |Fn| goes, as n goes to infinity, to
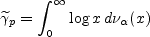where
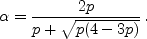
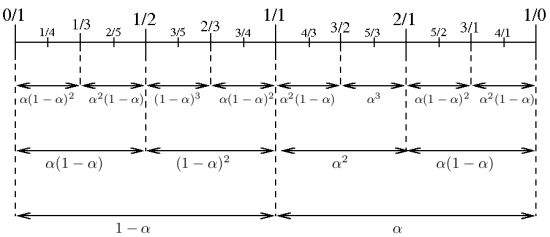
The measure 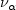on Stern-Brocot intervals of rank 1, 2, 3.
First assign mass 1 - α to [0,1] and α to [1,∞].
Once 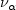is defined on some Stern-Brocot interval of rank r, a proportion α of its mass is given to the left (respectively right) subinterval of rank r+1 when r is odd (respectively even).
For p = 1, we get α = 1 both in the linear and the non-linear cases, and the measure 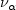is the Dirac mass on φ, where φ = (1 + √5)/2 is the golden ratio. This of course corresponds to the classical Fibonacci sequence.
For p = 1/2 (which corresponds to the case studied by Viswanath [3], we get α = 1/φ both in the linear and the non-linear cases. The measure 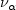is then equal to Viswanath's fractal measure conditioned on R+.
We also give some results about the variations of the largest Lyapunov exponent.
In the linear case, the largest Lyapunov exponent is a continuous, increasing function of p. In the non-linear case, the largest Lyapunov exponent is a continuous, non-decreasing function of p (increasing on [1/3,1]). In both cases, the derivative with respect to p for p=1 is equal to (log 5)/2. This value is obtained from a general formula we provide for the derivative with respect to α :
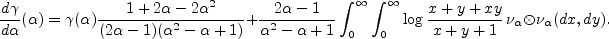
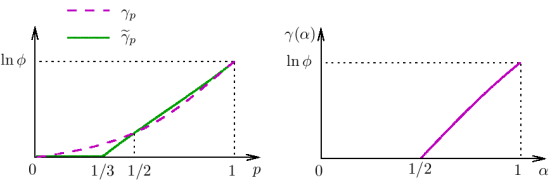
Graphs of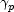 
and 
as a function of p (left) and as a function of α (right).
Notice that = 0 for p in ]0,1/3]. For p ≥ 1/3, the graph of is not the straight line it looks like: Compare the average slope with the derivative in 1.
Observe that in the non-linear case, the largest Lyapunov exponent is not an analytic function of p. This shows that, by contrast with the linear case, the non-linear random Fibonacci sequence can not be seen as a product of i.i.d. matrices.
The method we use does not rely on Furstenberg's formula [1, Chapter II]. We make use of some reduction properties of the random Fibonacci sequences, which were introduced by Benoît Rittaud in [2]. This reduction turns the sequence into a Markov chain, whose exponential growth is given with some elementary computations on continued fraction expansions.
Main references
[1] Philippe Bougerol and Jean Lacroix, Products of random matrices with applications to Schrödinger operators, Progress in Probability and Statistics, vol. 8, Birkhauser Boston Inc., Boston, MA, 1985.
[2] Benoît Rittaud, On the average growth of random Fibonacci sequences, Journal of Integer Sequences, Vol. 10 (2007), Article 07.2.4.
[3] Divakar Viswanath, Random Fibonacci sequences and the number 1.13198824..., Math. Comp. 69 (2000), no. 231, 1131-1155.
